Wheel 101;&#EMódulo de Young,-IMomento de inercia radial de la sección axial,-K InicializaciónMH – el coeficiente de rigidez del par correspondiente a la barra de conexión equivalente con una grieta completamente abierta. La ecuación tiene dos sumas - la flexibilidad relacionada con la grieta y la flexibilidad del haz libre de grietas.It
Cabe señalar que, independientemente de la forma del haz, las condiciones límite y la ubicación de la grieta La contribución a la flexibilidad general del haz depende únicamente del coeficiente K InicializaciónMH ,Primer resumen. Cuando el haz gira, la flexibilidad de la Sección de grieta cambia.Obtenemos la siguiente información:Wheel 101;
G O&#No hay grietas en la flexibilidad del haz Q()=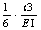
锿 Q
Sí.La rigidez del par de la barra de conexión equivalente sólo depende del diámetro del eje, las características del material y la profundidad de la grieta.La variación de la posición de la grieta en el eje y las características del eje (incluido el dispositivo de apoyo) no alteran la rigidez del par de la barra de conexión equivalente (parte superior)&#La Sección agrietada mantiene las mismas condiciones en cualquier parte de la sección agrietada a la que se dirigeObtain).Volviendo a la matriz de rigidez obtenida anteriormente, el coeficiente de rigidez se puede escribir como: Wheel
101; K
Inicialización
Ee , K Inicialización
Hmm. Valor inicial de la rigidez del momento en el eje correspondiente de la grieta completamente abierta&#. Tareas KInicialización Ee,KInicialización -Hmm.El cálculo se puede resolver de dos maneras.En primer lugar, el cálculo de la rigidez del momento de flexión en el programa de elementos finitos.En segundo lugar, aplicar la teoría de la mecánica de fracturas.Si se conocen la geometría, el diámetro del eje y las características del material de las grietas abiertas, se puede calcular el coeficiente de flexibilidad local de las grietas abiertas [7,10].
Algoritmo de simulación del sistema de rotores agrietados El coeficiente de rigidez de momento de la grieta se obtendrá mediante los siguientes pasos.1. Crear un modelo de rotor completo en un program a especial para analizar la dinámica del rotor (por ejemplo:Por ejemplo, en la dinámica R4).2. Destacar la parte del rotor agrietada. 3. La grieta divide el segmento del eje en dos subsistemas.Un enlace descrito por una matriz de variablesCoeficiente de rigidezNo.K (q)
,
J)]
Pedir prestado
La dimensión 6x6 se encuentra entre subsistemas.
4. Coeficiente inicial de rigidez del momento
K
Inicialización
Ee ,KInicializaciónHmm.La solución analítica de la grieta abierta se obtiene mediante el método dado.Arriba.Estos datos son los cálculos iniciales.Mientras tanto, se calculan los coeficientes de la matriz de rigidez de la barra de conexión simulada agrietada.
Cada sistema de rotoresQ.Ecuación de la matriz de Estado no lineal que describe el modelo dinámico no linealLa estructura del sistema de rotores es la siguiente: Wheel101;No.M [en inglés]
– matriz de coeficiente de inercia;
No. C [en inglés]
– matriz de amortiguación y coeficiente de giroscopio;No.K
[en inglés]
Matriz Coeficiente de rigidez; {&#U},{U},{U}– la aceleración, velocidad y desplazamiento de las vibraciones correspondientes;{-F()T()}&&Cualquier Tipo de carga dinámica - Interior y exterior.La matriz de rigidez de la barra de conexión equivalente puede dividirse en dos partes: constante y variable, como se muestra a continuación:No.&K CIncluido en la matriz de rigidez general de la estructuraNo.K[en inglés]Sistema.Matriz() [Q J] n,KPara calcularReacciones de enlaces no lineales:-Wheel101;
U Recepción ,
U Ray.– MuLa rotación real de la sección sobre el eje correspondiente.La ecuación de movimiento final del sistema es la siguienteSí.Las ecuaciones dadas pueden ser resueltas por métodos numéricos, como el método Runge.Método Kutta, método newmark, etc.Comparando la flexibilidad de los dos algoritmos, se demuestra la suficiencia del algoritmo.Haz de soporteGrietas obtenidas en el análisis de elementos finitosDe acuerdo con el algoritmo supuesto en la dinámica R4, se optimiza el sistema celular.La tarea de este trabajo es calcular la Deflexión de la sección transversal de la grieta bajo la acción de la fuerza unitaria en diferentes etapas de la grieta y la fuerza.La figura 3 muestra los resultados de la comprobación del algoritmo propuesto.Se compararon tres resultados:El método de elementos finitos (FEM) se utiliza para calcular la flexibilidad.La flexibilidad radial del modelo de haz agrietado se calcula en el método de elementos finitos.
Todo el rango de posición del ángulo de grieta;&#La flexibilidad se calculó utilizando la dinámica R4 y los datos iniciales se obtuvieron utilizando Fem.Valor inicial del parRigidez de la grieta completamente abiertaK InicializaciónEe, KInicialización
Hmm.Se obtiene resolviendo la ecuación (7).
K-Inicialización
MH-Y la flexibilidad radial del haz agrietado
GC-En la Dirección correspondiente, el método de elementos finitos se utiliza para el cálculo.De acuerdo con la ley (10), la rigidez del momento en la posición de la grieta angular media cambia de mínimo a máximo.
La flexibilidad se calcula utilizando la dinámica R4.Datos iniciales sobre la flexibilidad del momento de flexión de la grieta completamente abierta
-K-Ee
Inicialización , K-Hmm.
Inicialización[7,10] se obtiene analíticamente utilizando el algoritmo de mecánica de fracturas.El valor de la flexibilidad del momentoLa posición de la grieta angular media varía de un mínimo a un máximo de acuerdo con la ley (10).Fig. 3 Variación de la flexibilidad del haz en la Sección de grieta por revolución Resultados del cálculo de elementos finitosEl modelo está muy cerca del modelo dinámico R4.La diferencia entre los resultados calculados en condiciones iniciales y los resultados de elementos finitos es inferior al 1%.Al mismo tiempo, el cálculo analítico de la rigidez inicial es mucho más rápido y requiere menos tiempo de trabajo que el cálculo de elementos finitos, por lo que es más fácil de realizar.AUso. Geometría y parámetros del rotor agrietado Seleccione la geometría del rotor agrietado para mostrar las mejores ventajas del algoritmo, como se muestra en la Tabla 1Rotor con disco central, soporte en el extremo del eje.② ②②②
② ②-②②②②②②②②② ②
②
② ② ②-②-②-②
②
② ② ②

Título profesional: Product manager
Departamento: Market Department
Teléfono de la compañía: +86 021-59150215
E-mail: Contáctenos
Teléfono móvil: +86 13817160919
Sitio web: lanzhusuperalloy.spab2b.com
Dirección: No. 2800 Caoxin Road, Xuhang Town, Jiading District, Shanghai